量子力学之纠缠
每个人心中那股蓬勃的求知欲望,如同求偶的雄鸟一样,激励着世世代代的科学家们,探寻宇宙的奥秘之处。你想知道宇宙有多广阔吗?你想探讨世界万物能否无穷无尽地分割下去吗?咱们可从来没有停步过,始终在这永无止境的旅程中畅游。
回顾我们走过的路途吧!在宏大的宇宙尺度上,我们能够无比精妙地解读生活中的诸多自然现象,准确地计算出每个物体、天体乃至群星的运行规律。尤其是宇宙本身,无论它有多么神秘,我们已经可以对此把握自如了。
然而,当你的眼睛转向那些看不见摸不着的微观世界时,一切都会让你目瞪口呆。在我们日夜相伴的细小世界里,每天每刻都在发生着数不清、让人瞠目结舌的变化。纳米级别的量子力学,便是这个深不可测的微观世界的严谨主人。
量子纠缠:颠覆直觉
哎呀,咱们在智商这回事儿上跟爱因斯坦老兄确实还有点儿差距嘛。不过还好啦,在咱们活着这个时辰,那些个好汉们早已过五关斩六将,开拓出一片新天地了。您不见得非得学明白那些个公式是咋推算出来的,可您啥都不知道可不行,咱得弄清楚这个世界到底藏着些啥秘密。话说,理解量子纠缠,可不就意味着您离那暗藏玄机的答案越来越近咯。
下面我给大伙儿举个浅显易懂的例子吧,好多科普视频都喜欢用这个,简便明快,直接瞅一眼就懂。假设有俩小箱子,里头各塞了一副手套。您把其中一个搁家里头,另一个揣到南极去了。然后呢,待会儿你翻开家里那个箱子,看见里面是左手手套,那保准儿另外那个盒子里头也是右手手套,这事儿来得可是巧得很哦,没延误半秒钟。
是不是觉得挺容易?这道理别说小学生,幼儿园小朋友也听得懂。不过啊,大伙儿脑子里的量子纠缠可不是这么回事儿哟,这儿头儿摆着个天大的差别呐。
咱们这个简单的手套事儿,其实是可以从两方面来看的。前一种说法儿就是说,在你把眼睛瞅进那个破箱子之前,哪个手套在哪儿呆着,早就板上钉钉了。你看着是左手手套,其实那货就在那儿躺着等你查,谁都改变不了,这是客观事实,只是你自己不晓得罢了,跟你看没看压根儿没关系。这观念就是咱们平时常说的那种经典思维。
后一种呢,跟第一种恰恰相反。按照他们的看法,在你撩起箱子盖之前,里头有哪个手套可是悬念丛生的。要注意哈,这种悬念可不是由于你没瞧见,而是它本身就是那么悬乎。它处于一种左手手套和右手手套两种可能之间的混合态,到了你开箱子的那一刹那,它才立马一击即中,变成右手套。而且,它还给另一个手套传个信儿过去,嘱咐人家换左手套吧!结果就是,当你打开地球另一边的那个大箱子时,看到的自然是左手套。
这就是咱们今天要讲的量子世界观。您品,您细品,没摸索的事物就不会亮相展演,就像这个世界的地图,原来都是因为被人粗略看来,才慢慢勾勒出轮廓的呀。
跟经典思维比较起来啊,量子世界观给人们带来了一种难以言表的虚幻感。说实话,我们之前用手套来讲这个故事,说白了只是为了大伙儿能够更好地了解这个主题。对于手套这类大家伙儿来说,即使你不清楚,但是总归能有人,或许是个天才,或是计算机,或者别的什么玩意儿,他们都知道手套在被放进箱子前的模样。但是,微观世界中的那些个小家伙,比如说光、神奇的电子等等组成世界的基石粒子,它们小到没法子形容,要是咱们不去仔细地瞅瞅,那在这个浩渺无垠的宇宙之中,再也找不到一丝线索,没人知道这些个小东西到底长啥模样。
所以,你完全可以有理由去想一想,它在被观测前到底是明确无疑的状态呢,还是模糊不清的叠加态呢?说真的,这事情在好多年前可是引起了爱因斯坦和波尔两位大神的论战,争了足足几十年呢。这个激烈的观点碰撞正好发生在1935年,当时大名鼎鼎的阿尔伯特·爱因斯坦和他的小弟联手发表了一篇轰动科学界的论文《EPR悖论》。这篇文章中,字母命名的爱就是咱们的爱因斯坦爷爷。
EPR佯谬:爱因斯坦与波尔的世纪之争
首先儿咱们得把话说清楚哈:啊,咱们在这儿聊EPR佯谬这种事儿,首先得有个共识,微观领域那可是啥都有啊,可那啥是做不得假的哦!比如说啊,数学就是咱们的老大哥,那就服帖;还有实验那么准,那什么守恒定律,能量守恒啦、动量守恒啦、角动量守恒咱们都是必定遵守滴;除了这些老大们外在的规矩,剩下那些有的没的,咱都可以拍胸口问心无愧地大闹天宫,去怀疑人家。
说起这EPR佯谬嘛,本意是个思考实验,就是想测量两个粒子的动量和坐标,后来有人简单化处理了一番,就剩测量粒子自旋这一项了。哈,这实验就像唱大戏那样简简单单的,咱们想想看哈,有个粒子啊,它自旋总得是零吧,但是被某个妖怪整蛊了一下,分成两个小不点儿走了。这时候咱们把这俩小妖分开,一个跳西天过海,一个飘洋过海。等到它们离得千山万水时,咱再看看左边那个小妖的自旋,它就已经告诉咱了,例如上旋。咱这整个儿测量过程,可没给小妖施加半点力啊,那依照角动量守恒菩萨所言,右边那个小妖,它的自旋,肯定就是下旋无误了。
这玩意儿啊,跟咱们之前聊的手套里的小粒子本质上可是一回事儿。这事儿呀,也是有双面性的。量子力学那边就说,原来那俩小妖都是老老实实地没有自旋的,可是你非得强行测量他们的自旋的话,那他们就只能犹犹豫豫、忐忑不安地给你表演出个上旋来,于是,右边那个小妖也毫不客气地被拧成了一个确定无疑的下旋。可是爱因斯坦他老人家可不信这邪门歪道,他老人家琢磨,那俩小妖距离那么远,咋可能左边一摆右一摆的呢?一个小玩意儿,怎可能转眼间就能影响到千里之外,甚至是遥不可及的另一个小东西呢?这不就成妖精附体了吗?
于是乎,爱因斯坦斩钉截铁地认定,俩小妖在分离的那一刹那,他们的自旋方向就已经妥妥儿定下来了。你看到那个随机的结果,那是因为这里头藏着些不能见人的隐变量,搞得有时左边上旋右边下旋,有时右边上旋左边下旋。这隐变量让他们本来就是同生共死的,所以咱不需要什么超距之力嘛。你自以为随机看到的是个上旋的结果,那还不是因为你不懂这些虐猫虐狗的隐变量嘛,就好比气象台预报明天下雨的概率是70%,那可不代表明天下雨这件事就是纯粹瞎碰运气的,而是我们的消息渠道和技术装备实在是不够硬核不够全面。要是你能踩着七色云彩过几天,了解整个大气环流、地理走势、水汽扩散啥啥啥的复杂因素,那你肯定能精确无误算出明天下不下雨。这样的观点就叫隐变量论,这事儿牵扯到爱因斯坦的哲学信仰。爱因斯坦有句堪称经典的名言:“你以为没人看月球的时候,月亮就凭空消失了吗?”
好了,咱们闲话少说,这次你可能会站在爱因斯坦这边儿,毕竟他的见解看上去还是挺正常的玩意儿嘛。但波尔又站起来解释了,由于数学上这两个例子只能用同一个波函数来描述,那有没有一种可能,这两个例子本来就是一个整体呢?你的测量是在跟这个整体打交道,所以这不算超距作用。但是,这番解释听起来更像是诡辩的话术,难以让人信服。难道作为整体的两个例子,就不是一左一右的独立的两个例子吗?
所以,薛定谔后来略带嘲讽地说:“那这两个例子是纠缠在了一起吗?”于是,后人们便将这种诡魅般的现象称之为量子纠缠。但问题是,我们要如何证明谁对谁错呢?观察也不行,不观察也不行,这看起来似乎就是一个无法证伪的理论,诡魅般的超距作用从此成为了量子力学的命门。
但是呢,咱们人类的智慧却是不可小觑哒。哎呀,大概刚过去的那啥,快三十年的事儿吧,那个时候,一个名叫约翰·贝尔的神奇爱尔兰物理学家提出来了一个让人瞠目结舌的检验方式。简而言之,这个约翰·贝尔就提出了一个小小的贝尔不等式,硬是把爱因斯坦本来的隐变量理论给扭捏成了一个数学公式。要是咱们能用实实在在的实验去考验这个贝尔不等式,只要证明它成立,那爱因斯坦爷子就是对哒。
为了更好地理解这个贝尔不等式,咱们先来听听这么一个小故事吧。假设有这么一台机器,每隔一秒钟,就在左右两边同时发射出一个小球。这些小球就只有两种颜色,要么黑要么白。咱们两个每人站一头儿,把看到的小球颜色记在纸上。
为此么,咱们进行了这么几个小实验:
第一个实验题目:咱们两眼一抹黑,什么都不干,然后互相比对。结果怎么样呢?不管咱们盯它多长时间,收集到的两个小球儿颜色总是不同步。只要我那里收到一个黑色,你那儿接收到的绝对就是个白色。这说明了这台机器规律性的强大,它每次分别派出的两个小球们的颜色总是截然不同。
第二个实验题目:我这儿捣弄到了一副奇怪的眼镜,用来观察那些乒乓球,而你那边则继续保持原样。经过一段时间的观察,咱们发现竟然有1%的情况下,小球儿的颜色是一模一样的。为了屏蔽掉我本人的主观干扰,我干脆把眼镜拿给你戴上试试,可结果依然这样。看来啊,这眼镜肯定有什么毛病,它有1%的概率让你的眼睛看错了颜色。
第三个实验题目:咱们统统戴上那副眼镜。现在呢,请各位同学好好动脑筋回忆一下,估计你们已经猜出来了哈,这回,咱们统计的结果里,两个小球颜色一样的频率会是多少呢?这题其实挺容易的,我的出错率是1%,你也是1%,除非咱们俩正巧在同一时刻出了差错,不然总的出错率就只会是刚好2%啦。要是咱们同时出了错,那总的出错率就要少于2%啦。也就是说,咱们的出错率最多顶多也就2%这么点儿。
我们回到一个量子实验 斯特恩-盖拉赫实验,粒子的自旋
- 自旋方向并不是一个固定的方向,它取决于外部的测量方向。
- 对于已经知道自旋方向的粒子,换个角度
再次测量时,测出同一侧方向的概率严格满足这个式子
比如当
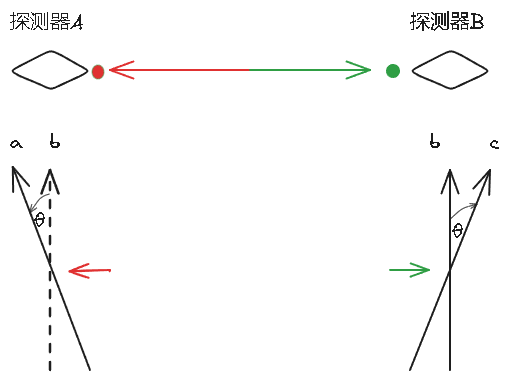
对于总自旋为 0,因衰变等原因分开的两个粒子,根据角动量守恒,它们的自旋方向始终相反。现在我们分别用两个探测器,检测它们的自旋方向。实验分三步:
- 两个探测器方向一致,那么测出来的结果,就始终是自旋方向相反(具体细节参考斯特恩-盖拉赫实验可以)。
- 探测器 A 向左倾斜一个夹角,则两个探测器测出同方向的概率(可以理解出错),就是
。同理探测器 A 不变,探测器 B 向右倾斜一个夹角,出错率也是一样 。 - 重点来了,当两个探测器同时倾斜,此时总出错率应该是多少?
正常来说这个出错率,不会超过两倍的
这其实就是贝尔不等式的一种简单表述。也就是说,如果我有 1% 的误差,你也有 1% 的误差,那我俩加起来总的误差不会超过 2%。这在数学上很好证明,这个不等式有个基本前提就是我的测量动作,并不会影响到你的测量结果。
如果我对左边粒子的观测动作,瞬间改变了右边粒子的自旋方向,那右边探测器的出错率,就不再是
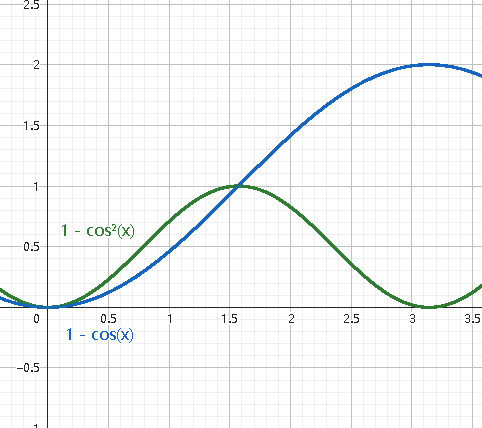
只要实验违反了贝尔不等式,说明自旋确实是在测量的时候才确定的,说明爱因斯坦错了,上帝真的在掷骰子。也说明两个粒子之间有一个超远距离的协调。
1972 年,美国物理学家约翰·克劳泽用光子做成了这个实验。但有人提出两个质疑:
- 有没有可能两个光子之间的确有协调,但那个协调速度并没有超光速呢?
- 有没有可能光子之间其实还是没协调,但光子的发射装置突然像是长了眼睛,它能事先看到两边测量仪器的角度,然后选择发不一样的光子呢?
1982年,那时的法国物理高手阿兰·阿斯佩接下了这块硬骨头——严密堵住那俩畏手畏脚的破绽。他一手操持了一台实验武器,这货儿有多牛呢?离地球到月亮那儿那么远,时间的误差又是小数点后头好几个零那种级别的精确度,就这么神奇地证明了:“两颗光子kiss的速度,得超过光速的2倍才能让你侬我侬,携手同行”。当然,这试验设备还有一个梗,就是阿斯佩发明了一招,让光子悠哉游哉走后,再让两端的探测器来个随机转头的大变活人,这就使得贝尔那条看似铁板钉钉的不等势,还是挨了狠狠一记耳光。紧接着,科学家们用更严格的招数,打得贝尔不等势更是狗不理包子,量子缠绕这玩意儿实实在在就出现了。
说到这儿,2022年那几位拿诺贝尔物理学奖的大神,大家都该认识了吧?就是那三位科学家,啥情况你们懂滴,就是他们在量子纠缠光子实验里给贝尔不等式打脸,开创了量子信息科学的新天地。于是乎,荣誉就归了量子纠缠。话说回来,量子纠缠确实存在,这就意味着,咱们可敬可爱的上帝先生,他的确在玩儿骰子。不过别怕,当我们看不见这些微观小伙伴时,它们其实就像是一团模糊的概率,啥也不是。所以嘛,我们看到的这世界,其实大部分是由自己照镜子看出来的哟。我们可不止是看客啊,恰恰相反,我们都是这个世界的马良大仙!可惜呀,当年爱因斯坦他老人家没能亲眼见证这个伟大时刻。1955年那个春天,他孤身一人离去了。爱因斯坦他一辈子都反对量子力学的主流解读,可是这并没有阻挡他对量子力学作出的巨大贡献。正因为这位物理巨匠的无数次那些严谨且关键的质疑,我们才逐步建立起来了今天这个的量子力学。
现在我们醒过神来了,原来量子纠缠其实并不违背相对论哦!因为这货儿就是一个路过的,啥都不给带。量子纠缠展现出那种像孙猴子一样蹦跶的非局域性,就算两个纠缠粒子被扔出去几个光年那么远,它们之间的互动也是马上到位,简直就像是空间的魔术师一样,这种非局域性挑战着我们对经典物理学中的地方性实体理论这种老观念,反常规。
在量子场论看来,纠缠就是他们共用一个场,场的量子波动在空间里溜达进出,勾搭成奸。把纠缠定义成是场的属性,而不是牵红绳搭鹊桥的粒子关系。量子场论这招看成了一个更全面更连续的视角,就好像给量子纠缠签发了一张通关证,去看看场的动态演出。
量子纠缠的影响
量子纠缠这东西儿可不是闹着玩儿的,它对咱们的科学技术搞出了个大动静。被用上了量子计算、量子通信加密这种高大上的科技领域里。首先说说这个量子计算吧,这可是个新鲜事物,它就是顺着量子力学的原理搞点儿事儿,搞玩意儿。大家都知道,这量子计算的速度比起咱们平常使的那一套要快多了,为啥呢?因为它能一口气儿处理海量的数据。
然后聊聊量子通信,这也是个新鲜东西,它就是凭着量子力学的原理搞通信。量子通信的优点多得数不过来,就拿安全性来说,那简直就是甩了传统通信一条街啊,因为它能防止别人偷听你说话!最后说一下量子加密,这又是个新东西,它是用量子力学的原理搞加密。它的安全性比普通加密方式高出许多台阶,因为它能防止密码被人破译。
除了这些,还有很多其他领域可以用到量子纠缠,比如量子成像、量子传感和量子计量等等。量子纠缠真的是个大发现,对我们的科技革命起到的推动作用不可小觑。而随着对量子纠缠的深入研究,肯定会发现越来越多关于它的妙处,而且还可能开拓更广阔的应用天地。